[논문 정리] Generative Adversarial Networks
GAN 논문의 수식적 정리를 해보려 한다. 수식과 이미지는 원 논문과 최윤제 님의 자료를 참고 및 첨부하였다. 틀린 부분이나 빠뜨린 부분은 향후 지속적으로 보강할 예정이다. GAN의 컨셉은 원 데이터 X의 분포를 학습하려는 G 와 이로부터, 생성된 데이터 G(z)와 진짜 데이터 X를 구분해내는 D를 번갈아가며 학습하는 것이다.
GAN이 이전에 포스팅했던 VAE와 같이, Generative Model이기 때문에, Generator를 학습시키고 싶은 것이고, 수식적으로는 p(x)에 근사하는, generator distribution p_g(x)를 구하고 싶은 것이다. 이를 구하기 위해, prior noise variable z가 p_z에서 샘플링되고, 이를 deterministic function G(.) 를 통해 random variable를 생성한다. deterministic_mapper(random variable) = random variable
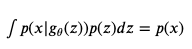
이 때, D와 G는 상반된 이해관계를 가지고 있으며, 이에 따라 하나의 목적함수에 최대/최소화 문제가 동시에 등장하는 minmax optimization 이 된다.
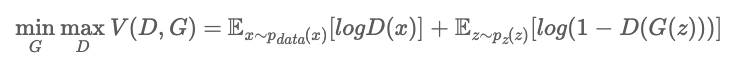
해당 value function을 최적화해주는 방식은, 아래와 같이 Discriminator 에 대해 weight 업데이트를 먼저 해주고, Generator에 대해서도 weight update를 번갈아가며 해주게 된다.

우리가 원하는 것은, Generator를 통해 나오는 G(z) 값이 P_data 의 좋은 estimator가 되기를 기대하며, 해당 조건이 충족하면서 converge 하는지에 대해 확인해야 한다. 이에 대한 optimality를 논문을 따라가며 체크해보자.
Global Optimality
첫 번째로 임의의 G에 대해서 D가 어떤 최적해를 가지는지 확인한다. 수식을 하나씩 살펴보자.

위의 식은 이전에 언급한 Value Function의 Expectation을 적분의 형태로 표현한 것이다. 이 때, 하나의 적분으로 묶으주기 위해서, 우변의 p_z(z)부분을 p_g(x)로 바꿔주게 된다. 즉, 아래의 등식이 성립한다. 그 이유는, 이전에 언급했듯 Generator의 목적이 p(x)에 근사하는 p_g(x)를 구하는 것인데, 이를 구하기 위해, G(p_z(z))가 사용되기 때문이다.

이렇게 하나의 적분에 두 식을 감싸놓고 최적화문제를 풀면 되는데, 아래처럼 치환하여 간단하게 풀면 된다.
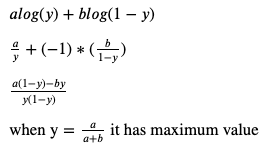
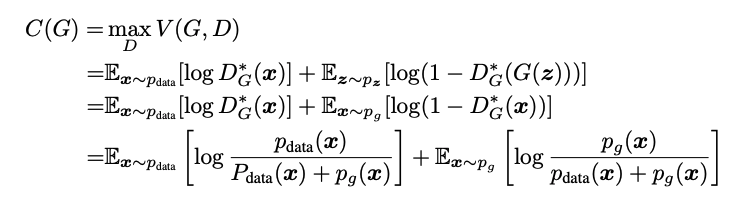
D가 최적인 식을 구하면, 이제 G에 대한 식으로 바뀌게 된다. 이제 C(G) 를 minimize 하는 문제를 풀면 된다. C(G)를 푸는 문제는 Jensen-Shannon divergence까지 가는 일련의 과정이다. 복잡해보이지만, 위에서 계산한 optimal D식을 a/(a+b) 식으로 바꾸기만 하고 풀면 마지막까지 도달할 수 있다.
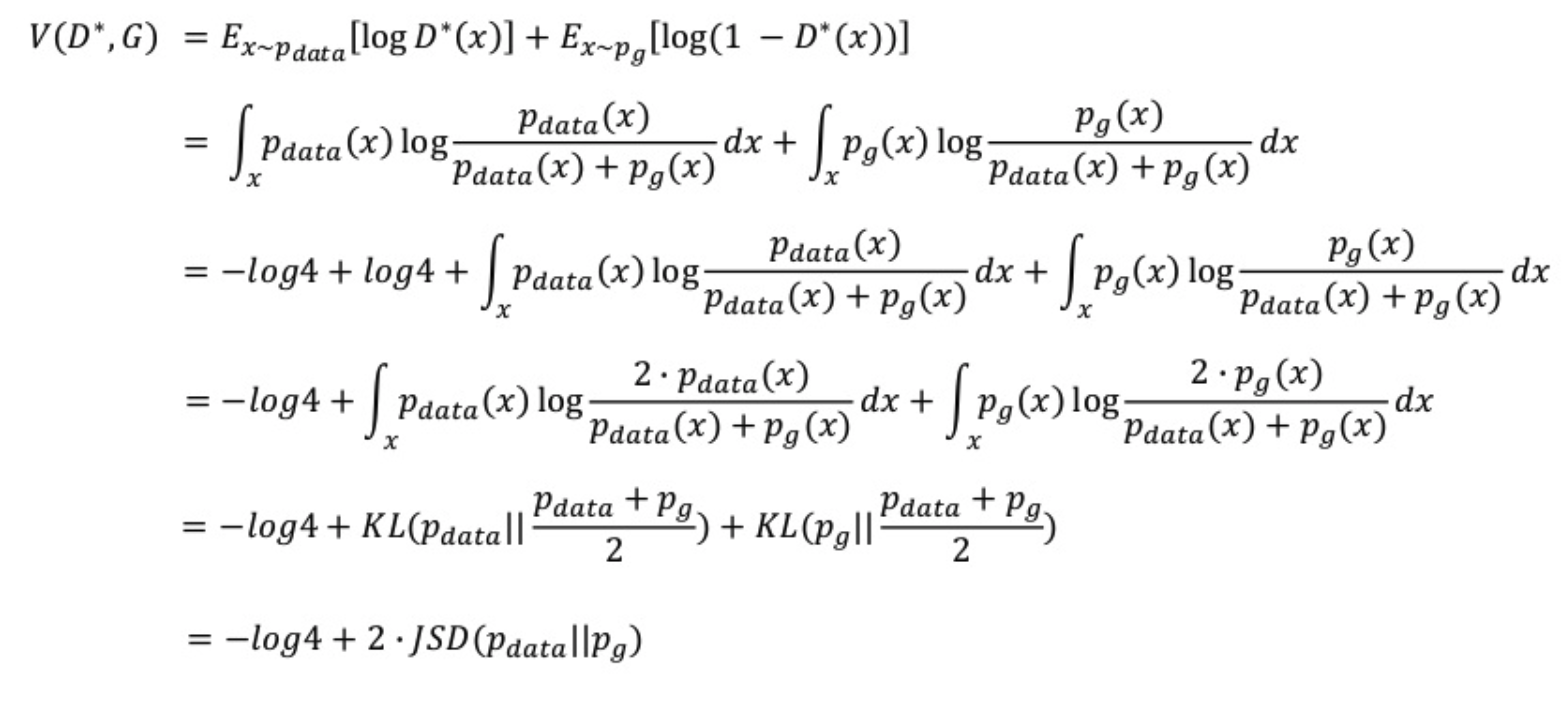
결국 위 식이 의미하는 것은, optimal discriminator 에 대해서 최적의 value function을 얻는 방법은, p_data 분포와 정확히 일치하는 p_g 분포를 만드는 것이고 이 때, value function 값은 최소값으로 -log4임을 알 수 있다.