[간단 정리] model calibration 에 대해 알아보자 (2)
지난 1편에 이어, 이번에는 model calibration 에 대한 기법들을 알아보려 한다. model calibration 기법은 크게 두 개로 나뉘어질 수 있다.
1. 모델을 학습한 후 (train-set), calibration post-processing 진행 (validate-set)
2. 모델을 학습할 때, calibration method 동시에 학습 (train-set), calibration method 에 대한 hyper-parameter tuning (validate-set)
이번에 다뤄보려고 하는 것은, 위의 1번에 해당하는 post-processing 기법이며 특히 sklearn.calibration.CalibratedClassifierCV 모듈에 있는 기법인 'sigmoid' 와 'isotonic' 에 대해 알아본다.
참고한 논문은 Alexandru Niculescu-Mizil and Rich Caruana (2005) Predicting Good Probabilities With Supervised Learning, in Proceedings of the 22nd International Conference on Machine Learning (ICML) 으로 두 기법에 대한 overview 가 매우 잘 이뤄져있다.
이 두 방법을 하나씩 이야기하기 전에, 공통적인 것들을 다뤄보자. 해당 방법은 validate dataset 을 사용하며, 모델의 predicted probability 를 입력값으로 하고 class label 을 결과값으로 하는 task 이다. 내가 이해한 데로 해당 task 를 이해해보자면 해당 예시를 쓸 수 있다. 내 친구 중에 뭐든 자신만만하게 하는 친구가 있다고 하자. 그걸 항상 옆에서 들어온 나는, 친구가 "이번에 A 가 B 할 확률이 90% 이상이야!" 라고 하면 옆에서 듣는 나는 '좀 그럴 듯 한가보다..' 이러면서 대략 60%로 조정 (쉽게 말하면 걸러 듣는다.) 할 것이다.
다시 돌아와서 보면, post-processing task 는 모델이 학습된 training dataset 이 아닌, validate dataset에서 predicted probability가 well-calibrated 되도록 조정하는 과정을 의미한다. 해당 regression task 는 모델 예측의 방향을 바꾸지 않고, probability 의 순서를 재정렬하지 않기 때문에, accuracy 와 같은 performance 에는 영향을 주지 않는다. 다만, 그 confidence 의 "정도" 만을 바꾸게 된다.
이제 하나씩 보면서 이야기를 더 해나가보자
1. Sigmoid
많이 들어본 sigmoid 이다. binary classification 을 할 때, 최종으로 나온 1X1 크기의 logit 을 [0,1] 으로 조정해줄 때, 사용한다. 자연지수 항이 붙어있기 때문에, 값이 커질 수록, 기하급수적으로 큰 확률값의 형태가 반환된다.
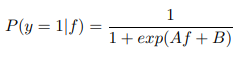
이제 predicted probability 를 validate dataset 에서 볼 수 있는 class label 로 재학습을 시켜야 한다. train dataset 으로 하지 않는 이유는, 애초에 mis-calibration 은 train dataset 에 class label 에 model 의 logit 또는 probability output 이 overfitting 되었기 때문이다. loss function 은 neural network 학습에서 흔히 볼 수 있는 binary cross-entropy 를 사용한다.
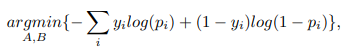
흥미로운 점은, 단순 이산변수를 class label 로 쓰는 것이 아닌, 확률값의 형태로 약간 smoothing 된 값을 사용하는데, 각 label 별로 opposite label 에 대한 확률을 조금씩 부여해준 것이다. 이는 bias 를 줄이고 일반화를 높여 overfitting 을 방지하겠다는 이유인데, 아래의 식은 positive 와 negative 각각, a=b=1 로 둔 beta distribution 의 평균값을 의미한다. (negative 의 경우 positive 에 따라 나온 식에서 1을 빼줘서 opposite 하게 만들어준 것이다.)
(이를 보면서, label smoothing 이 neural network 에 일반화에 큰 기여를 한 것이 bayesian inference 관점에서의 맥락을 지니고 있는 것이 아닐까 라는 생각이 들었다.)

최종적으로 gradient 를 계산해서 back-propagationt 을 통해 sigmoid 에 있는 A,B weight 를 업데이트해주면 된다.
아래는 실제 sklearn.calibration에서 sigmoid 에 대한 최적화 소스 코드이다. 처음에 각 class label 을 Bayesian prior 의 형태로 바꿔주고, objective 라는 함수에서 binary cross entropy loss 를 계산하며, grad 에서는 sigmoid 에 있는 A,B에 대한 gradient 를 계산해주어, scipy.optimize.fmin_bfgs 모듈을 통해 최적화하는 것을 볼 수 있다.
predictions = column_or_1d(predictions)
y = column_or_1d(y)
F = predictions # F follows Platt's notations
# Bayesian priors (see Platt end of section 2.2)
prior0 = float(np.sum(y <= 0))
prior1 = y.shape[0] - prior0
T = np.zeros(y.shape)
T[y > 0] = (prior1 + 1.0) / (prior1 + 2.0)
T[y <= 0] = 1.0 / (prior0 + 2.0)
T1 = 1.0 - T
def objective(AB):
# From Platt (beginning of Section 2.2)
P = expit(-(AB[0] * F + AB[1]))
loss = -(xlogy(T, P) + xlogy(T1, 1.0 - P))
if sample_weight is not None:
return (sample_weight * loss).sum()
else:
return loss.sum()
def grad(AB):
# gradient of the objective function
P = expit(-(AB[0] * F + AB[1]))
TEP_minus_T1P = T - P
if sample_weight is not None:
TEP_minus_T1P *= sample_weight
dA = np.dot(TEP_minus_T1P, F)
dB = np.sum(TEP_minus_T1P)
return np.array([dA, dB])
AB0 = np.array([0.0, log((prior0 + 1.0) / (prior1 + 1.0))])
AB_ = fmin_bfgs(objective, AB0, fprime=grad, disp=False)
return AB_[0], AB_[1]2. Isotonic
Isotonic regression 은 위의 sigmoid 보다 더 간단하며, 더 일반화된 식을 사용한다. 아래의 두 식에서 m을 학습시키는 mean squared 를 최소화하는 linear regression task 이다. 이전의 sigmoid 는 상하방이 [0,1] 로 막혀있고, 지수승이 들어있는 형태였지만, Isotonic 의 경우 선형식이기 때문에, stepwise 한 성질을 띄고 있고, 식이 결과값에 대한 제약이 없기 때문에(상,하방이 뚫려있다..!!), 적은 데이터에 대해 sigmoid 보다 overfitting 이 취약하다고 알려져 있다.
(실제로 sklearn 에서 sigmoid calibration 을 권장하고 있다.)

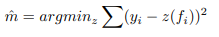
Isotonic regression 을 푸는 알고리즘 중 하나인 PAV algorithm 이 있다. 이는 위의 식과 같이 선형적인 관계로 만들기 보다, interpolation 을 통해 옆에 있는 값들을 계단식으로 동일하게 맞춰주면서, 근사적인 선형관계를 만들어준다.

PAV algorithm 의 일부반 발췌한 소스코드를 보면, interplation 을 사용하고 있음을 알 수 있다.
def _build_f(self, X, y):
"""Build the f_ interp1d function."""
# Handle the out_of_bounds argument by setting bounds_error
if self.out_of_bounds not in ["raise", "nan", "clip"]:
raise ValueError(
"The argument ``out_of_bounds`` must be in "
"'nan', 'clip', 'raise'; got {0}".format(self.out_of_bounds)
)
bounds_error = self.out_of_bounds == "raise"
if len(y) == 1:
# single y, constant prediction
self.f_ = lambda x: y.repeat(x.shape)
else:
self.f_ = interpolate.interp1d(
X, y, kind="linear", bounds_error=bounds_error
)
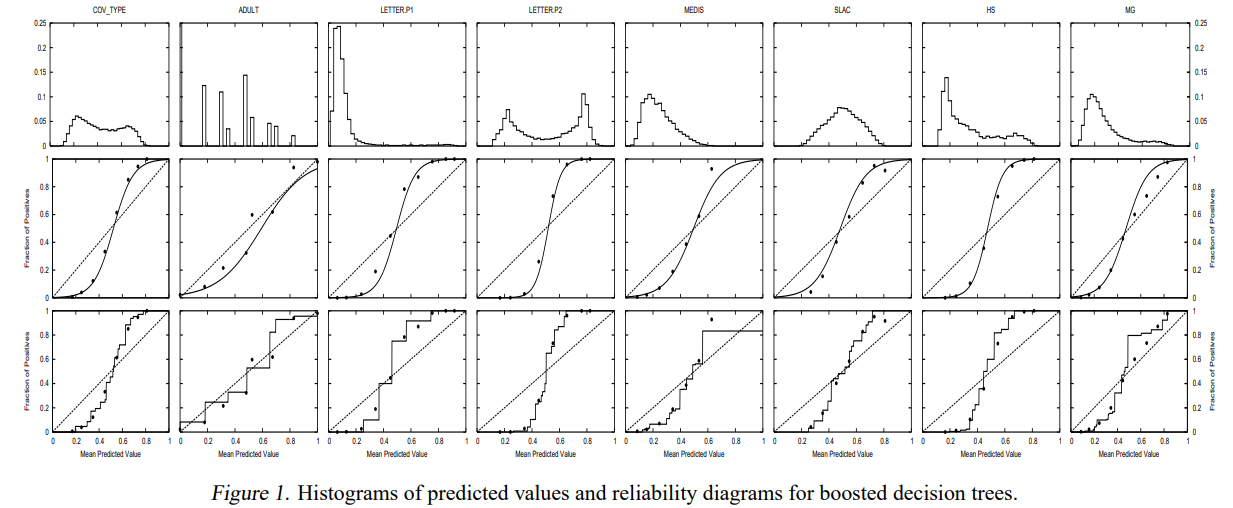
보다 쉬운 이해를 위해 참고 논문에 첨부된 이미지를 보면, 제일 윗 행이 input 이 되는 predicted probability이며, 순서대로 sigmoid 와 PAV algo 에 따른 isotonic regression에 따른 fitting 결과이다.
sklearn.calibration 모듈에서 지원하는 두 방법론인 "sigmoid"와 "isotonic" 에 대해 알아보았다. 해당 방법론은 현재까지 효율적으로 사용되고 있으며, 그 방법도 간단한 편이다.
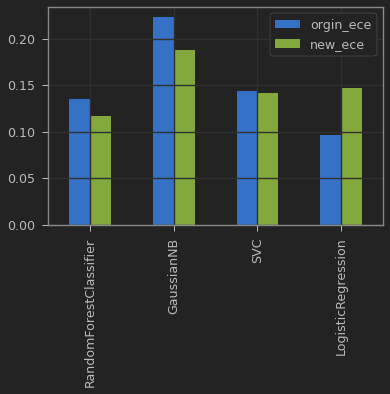
함께 이야기해본 방법론 중, "sigmoid" 방법론에 대해서 toy data 로 실험을 해보았고, 결과는 아래와 같다. 데이터는 널리 쓰이는 토이 데이터 'diabetes' 이고, 이진 분류 문제이다. 왼쪽의 파란 bar 는 calibration 전이고, 오른쪽은 sigmoid 를 통한, calibration을 하고 난 후이다.
logistic regression 을 제외한 나머지 방법론에 있어서 크고 작은 ECE 감소를 확인할 수 있었다. 참고로 SVC 의 경우 원래 logit 을 반환하는 모델이지만, probability=True 옵션을 주면, 내부적으로 sigmoid calibration 을 진행한다고 한다. sigmoid scaling 을 통한 방법론을 Platt 이 제시해서, 본문에는 Platt scaling이라고 명시되어 있다. 이에 따라 (이미 같은 방법론으로 calibration 을 했음), SVC 의 경우 성능 변화가 거의 보이지 않는다.
Logistic Regression 의 경우가 가장 흥미로웠는데, logistic regression 은 애초에 log loss 를 사용하여 학습을 시키기 때문에, 자체적으로 well-calibrated 한 모델이며, 이 경우 sigmoid calibration 은 역효과를 낫는 것으로 보인다.
두 번째 포스팅을 위한 방법론을 다루면서 느낀 것은, 이 방법론은 결국 모델의 over/under - confidence 를 고치지 못한다는 점이었다. 즉, 학습한 모델은 결국 스스로 결정에 대한 확신을 제대로 학습하지 못하고, 다른 보조 모델을 따로 두어야 한다는 것인데, 무언가 본질적인 해결책은 아닌 것 같다는 생각이 들었다. model calibration에 대한 연구는 model generalization 과도 긴밀히 연결되기 때문에, 학습 과정에서 well-calibrated 을 지향하는 것이 좀 더 advanced 라고 생각하여 이에 대해 조금 더 알아보려 한다.
또한, 참고한 논문에 따르면, neural network 은 기본적으로 well-calibrated 라고 되어 있는데, 이 논문이 나온 2005년도 기준에서는 deep 한 network 가 없어서 그런 경향이 띄었던 것이고, 최근의 neural network 에서는 over-confidence 와 같은 mis-calibration 이슈가 많이 등장한다. 그 이유는 무엇이고 이를 해결하기 위한 방법론들이 무엇이 있는지 다음 포스팅에서 알아보도록 하겠다.