Identity Mappings in Deep Residual Networks
논문 : 링크
residual network 의 수식 표현은 아래와 같다.
$y_l = h(x_l) + F(x_l, W_l)$
$x_{l+1} = f(y_l)$
residual learning을 처음 제시했던 논문 에서는 $h$ 는 identity mapping 이었고, $f$ 는 ReLU 였다.
해당 논문에서는 $h, f$ 를 identity 로 만드는 것이 최적화를 쉽게 만들어주고 이에 따른 모델 성능 부스트에 효과적임을 보인다.
우선 $h, f$ 를 identity 로 만드는 것이 최적화를 쉽게 만들어주는 것에 대한 수식적 접근을 보면 아래와 같다.
위에 쓴 식에서 $h, f = \mathbb{I}$ 라고 하면 아래와 같이 단순해진다.
$x_{l+1} = x_l + F(x_l, W_l)$
이 식은 일종의 재귀식 형태를 띄는데 일반화하면 아래와 같다. 가장 마지막 layer 의 표현 $x_L$은 임의의 $l$ 번째 layer 표현 $x_l$ 에서 그 사이에 있는 residual 표현들을 더한 것과 같다.
$x_L = x_l + \sum_{i=l}^{L-1}F(x_i, W_i)$
이게 최적화을 쉽게 만드는 데에 어떻게 도움이 되는지는 미분식을 보면 된다. loss function의 값을 $\epsilon$ 이라고 할 때, 이 값을 $x_l$ 에 대해 미분하면 아래와 같다.
$\frac{\partial \epsilon}{\partial x_l} = \frac{\partial \epsilon}{\partial x_L} \frac{\partial x_L}{\partial x_l} = \frac{\partial \epsilon}{\partial x_L} (1+\frac{\partial}{\partial x_l} \sum_{i=l}^{L-1}F(x_i, W_i))$
위 식을 보면 $ \frac{\partial \epsilon}{\partial x_L}$ term 이 더해져 있음을 확인할 수 있다. 즉, 몇 번째 layer 와는 상관없이 마지막 표현에 대한 loss 값의 미분값이 gradient 로 더해지는 것이다.
이는 skip connection 에 따라 $x_l$ 에 대한 정보가 $x_{l+1}$ 로 directly forward propagate 되는 것뿐만 아니라, 업데이트 과정에서는 directly backward propagate 되는 것을 의미한다.
또한, residual learning 을 사용하지 않는 plain network 의 경우 각 layer 의 gradient 가 chain rule 에 따라 곱해지는 형태를 띄었다면, 이 경우 gradient 가 더해져 있는 형태이기에 gradient vanishing 또한 더 적게 발생함을 알 수 있다.
gradient vanishing 이 발생하려면 $\frac{\partial}{\partial x_l} \sum_{i=l}^{L-1}F(x_i, W_i) = -1$ 이 되어야 하는데,
$\frac{\partial}{\partial x_l} \Pi_{i=l}^{L-1}F(x_i, W_i)$ 의 경우 각 layer의 gradient 가 1보다 작은 경우 0에 가까워지는 것이 맞지만, 우리의 경우(summation)의 경우 해당 값이 -1이 되어야 할 특정한 이유가 없기 때문이다.
On the Importance of Identity Skip Connections
이 섹션에서는 $h(\cdot)$ 이 identity mapping 이 optimal 인지를 확인한다.

이전 layer 의 값을 그대로 더해주는 것이 아닌, gating 을 하는 등의 시도를 한다. 이걸 수식으로 확인해보자.
scaling 을 통한 gating 의 경우엔 아래와 같다.
$x_L = (\Pi_{i=1}^{L-1} \lambda_i) x_l + \sum_{i=l}^{L-1} (\Pi_{i=1}^{L-1} \lambda_i) F(x_i, W_i) = (\Pi_{i=1}^{L-1} \lambda_i) x_l + \sum_{i=l}^{L-1} \hat{F}(x_i, W_i)$
$\frac{\partial \epsilon}{\partial x_l} = \frac{\partial \epsilon}{\partial x_L} ((\Pi_{i=1}^{L-1} \lambda_i)+\frac{\partial}{\partial x_l} \sum_{i=l}^{L-1}F(x_i, W_i))$
1 x 1 convolution 과 같은 보다 복잡한 변환은 아래와 같이 표현 가능하다.
$\frac{\partial \epsilon}{\partial x_l} = \frac{\partial \epsilon}{\partial x_L} ((\Pi_{i=1}^{L-1} h^`_i)+\frac{\partial}{\partial x_l} \sum_{i=l}^{L-1}F(x_i, W_i))$
결과는 identity mapping 이 가장 좋다. gating 이나 complicated transforms 들을 수렴이 잘 되지 않거나 degradation 이 발생하였다. 저자는 이러한 시도들은 더 많은 parameter 를 사용하여 representational ability 가 상승하는 것을 기대해볼 법 하였지만, 이를 통한 gain 보다는 optimizational issue 에 따른 loss 가 더 크기에 identity mapping 보다 outperform 하지 못한 것으로 보았다.
On the Usage of Activation Functions
위의 수식적 접근에서 본 것과 같이 최적화를 용이하게 만들기 위해서는 무엇보다 $f(\cdot) = \mathbb{1}$ 이 되어야 하는데, 해당 설정을 만들기 위해 도입한 pre-activation에 대해 알아본다.

(a) 는 이전 논문에서 제시한 구조이다.
우선 (c) 를 보자
일단 addition 뒤에 존재하던 ReLU 를 $F(x)$ 안에 넣는 것은 이해가 된다. 하지만 왜 pre-activation 까지 간 것일까? 우선 ReLU 를 $F(x)$ 안에 넣는 것이 위 그림의 (c) 인 ReLU before addition 인데, 이 경우엔 $x_{l+1}$ 의 파라미터가 $l$ 이 커져감에 따라 양의 방향으로 계속 커지게 되고, 이에 따라 표현력에 한계가 생기는 문제가 있다. (실제로 성능이 낮음)
이젠 (b)를 보자
(b) 버전은 일부러 addition 뒤에 activation을 없애려는 시도의 반대 방향의 실험을 한 것이다. addition 뒤에 BN, ReLU activation 을 넣게 되면 기존 (a) 보다 성능이 많이 감소하게 된다고 한다. 즉, addition 뒤에는 activation 이 없거나 normalization 과 같은 강한 signal manipulation 이 없는 것이 좋다는 것을 보인다.
(d) 는 (a) 버전의 asymmetric 버전인데, 이미지와 동일한 residual unit 이 아래 하나 더 쌓여있다고 생각해보자. 그러면 (d) 는 (a) 의 가장 밑에 있는 ReLU activation 이 $x$ 와 $F(x)$ 의 공동 레인이 아닌 $F(x)$ 에 대한 레인에만 존재하는 버전임을 알 수 있다. 즉, skip connection 에는 activation 이 없고 $F(x)$ 에만 적용되는 버전이라는 것이다. $F(x) + x$ 에 대해 activation을 적용하는 것이 표현력을 높게 만들어준다면 activation을 적용하되 $F(x)$ 에만 적용하고 skip connection은 clear information 만을 전달하자는 것이다. 이 또한 identity mapping 아이디어의 선 상에 있다.
그런 관점에서 (e)는 (b)의 asymmetric 버전임을 알 수 있다.
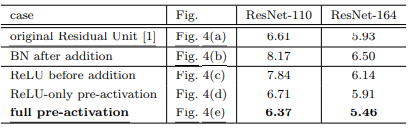
성능은 full pre-activation 이 제일 좋은데 그 이유는 activation 에 따른 representational ability 를 최대한 활용함과 동시에 residual learning with identity mapping을 통한 최적화의 이점까지 가져갈 수 있기 때문이다.
논문에서 저자는 pre-activation 을 통한 identity mapping 은 특히 extremely deep layer network 에서 효과적이라고 하였는데, 이전 논문에서는 1000개가 넣는 layer network 에서의 test error 가 100개 정도의 layer network 보다 높은 현상이 나타났다. 하지만 pre-activation 을 사용한 이번 모델의 경우에는 1000개가 넘은 layer network 에서 점점 그 성능이 향상되는 scaling effect 를 확인할 수 있다고 하였다.
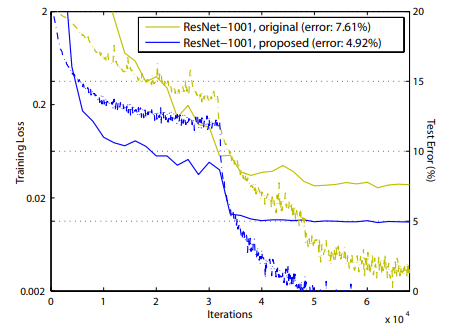
해당 논문은 identity mapping 을 통한 residual connection 의 효과를 확인하고 이를 위한 network 구성을 만드는 것에 집중한다.
한가지 궁금한 점이 드는 것이 있는데, attention is all you need paper 를 보면 post-activation을 사용한다. LayerNorm(x + Sublayer(x)) 해당 논문에 따르면 마지막 단의 ReLU 가 없는 (b) 버전이다.
물론 여기는 batch normalization 이 아닌 layer normalization 을 써서 상황이 여러모로 동일하지는 않지만, 왜 여기서는 post-activation을 사용한 것일까? network 의 형태에 따라 그 효과가 다르게 나타날까? 아니면 normalization 기법에 따라 다른 것일까? normalization 쪽을 들여다봐야할 수도 있겠다.