TechY
[간단 정리] model calibration 에 대해 알아보자 (3) 본문
calibration 1편에서는 calibration 이란 무엇인지와 주로 사용되는 metric 에 대해 다루었고, calibration 2편에서는 고전적인 calibration 방식이자 sklearn.calibration module 이 지원하는 방법론인 sigmoid 와 isotonic method 에 대해 알아봤다.
이번에는 딥러닝에서 사용되는 calibration method 에 대해 알아보려 한다. 참고한 논문은 아래와 같다.
- On Calibration of Modern Neural Networks [링크]
- Calibrating Deep Neural Networks using Focal Loss [링크]
- On Mixup Training: Improved Calibration and Predictive Uncertainty for Deep Neural Networks [링크]
- When Does Label Smoothing Help? [링크]
- Regularizing Neural Networks By Penalizing Confident Output Distributions [링크]
2편에서 다뤘던 논문인 "Predicting Good Probabilities With Supervised Learning" 논문에서는 neural network 모델이 well-calibrated 되어 있다고 이야기한다. 그 이유는 해당 모델을 학습할 때, log loss 를 최적화하는 loss function 을 사용해서 인데, 위에서 인용한 논문1에서 deep neural network 의 경우 poorly-calibrated 됨을 보여준다.
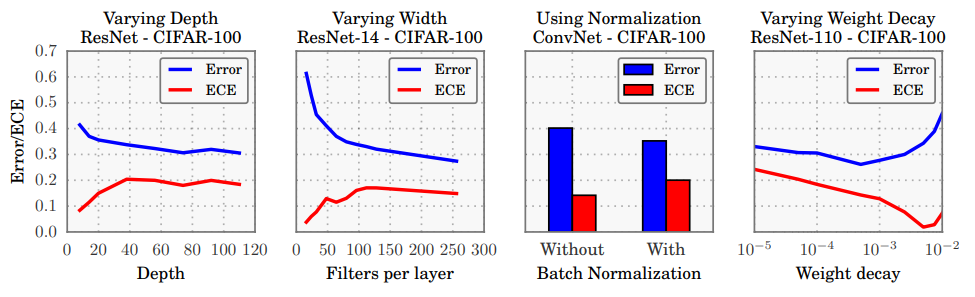
위의 이미지를 보면, network 의 capacity(depth, width)와 regularization(batch normalization, weight decay) 에 따라, calibration 성능의 경향성을 보여주고 있다. 재밌는 부분은 classification error (ratio of mis-classified) 부분은 계속해서 최적화되고 있음에도, calibration 에 대한 성능은 악화되고 있다는 것이다.
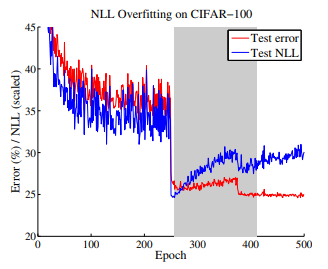
위 그림을 보면, 특정 epoch 이후에 test accuracy error 는 계속 낮아지는데, test log loss 는 계속 높아지는 것을 볼 수 있다. 이는, 우리가 사용하는 log loss 최적화가 likelihood 가 아닌, accuracy 를 높이는 것에, 과적합되고 있음을 시사한다.
어떻게 이런 일이 발생할까. 논문1에서는 model 의 capacity와 약간 regularization 이 이에 기여한다고 하면서, DNN의 overfitting 과 관련된 것들로 이유를 채운다. 논문2에서는 논문1의 이유를 보강하는 3가지 이유를 제시했는데 아래와 같다.
- Curse of misclassfied samples : in-sample NLL 에 overfitting 되어서, test NLL 이 오르는 것이다.
- Peak at the wrong place : mis-classified sample 에 대해 낮은 엔트로피 (높은 confidence) 의 값을 할당한다.
- Weight magnification : over-confident 는 parameter weight 의 norm 에 양의 관계가 있다. (논문 1에서도 weight decay 를 약하게 걸 수록 ECE 가 높아진다.) NLL 이 one hot vector label 을 학습하면서, penultimate layer (fc layer) 가 가질 수 있는 l2 norm 은 무한대로 간다. -> 이것이 주된 원인이다.

전반적으로 요약을 해보자면, DNN은 훌륭한 in-sample fitting machine 인데, 이 때, one hot vector label 을 사용해, NLL 최소화를 목적으로 학습시키면, softmax/sigmoid 을 통과한 output 이 one host vector 와 같이, 매우 뾰족한 형태가 되고, 이를 위해 parameter 가 학습되어 pooly-generalized/calibrated 가 된다! 라는 것이다.
문제를 알았으니, 해당 문제를 해결하기 위한 방법들을 알아보자.
Temperature Scaling
논문1이 제시한 방법론으로, 매우 간단해 많이 사용된다. 기존에 많이 사용되는 calibration 방법들이 scaling 에 기반한 것은 착안하여, scalar (>1) 값을 가진 scalar 로 마지막 logit 값을 나눠주고, softmax/sigmoid 를 통과시키는, 가장 간단한 방식의 scaling 을 한다. softmax/sigmoid 가 exponential 하기 때문에, 큰 값에 민감하게 반응하며, 같은 방식으로 조금만 그 값을 줄여도 그 값이 기하급수적으로 준다. 따라서 scale 방식은 vector norm 을 줄이고, over-confidence 를 줄이는 데에 효과적이다. 또한, 양의 값으로 나눠주기 때문에, classification error 에 영향을 주지 않는다.
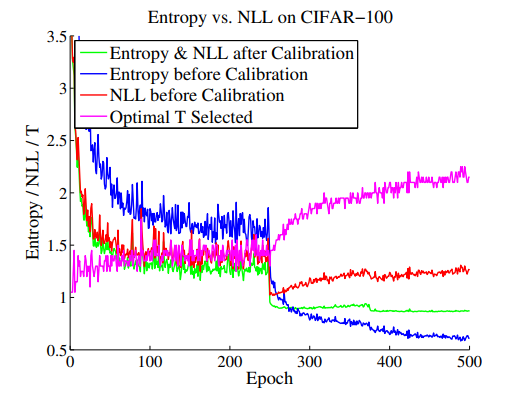
아래의 표를 보면, validation set 에서, temperature scaling 후, entropy 값이 늘고, test nll 을 낮춰줌을 확인할 수 있다. entropy 와 nll 이 하나의 선으로 표현된 이유는, 두 값이 같아지는 scaling hyperparameter lambda 를 사용했기 때문이다. 즉, 해당 값 또한 fitting 된 것으로 test dataset 에서는 다르다.
Label Smoothing
모델 일반화에 많이 사용되는 테크닉으로, target variable 을 [0,1] 의 값만 가지게 하는 것이 아닌, true index 를 제외한 나머지 class index 에도 값들을 조금씩 나누어주는 형태이다. 이렇게 하면, NLL 이 타겟하는 label vector 의 entropy 가 상태적으로 높아지면서 이에 따른 over-confidence 가 줄어든다. hyperparameter alpha 값으로 smoothing 의 정도를 결정하며, 높을 수록 정답 class label 의 1을 더 많이 나눠준다고 생각하면 된다. 아래의 plot 을 보면, temperature scaling 과 함께 label smoothing 을 사용해준 경우의 calibration 이 가장 효과적이었음을 볼 수 있다.

Entropy Regularized Loss (ERL)
해당 방법론은 predicted probability 에 명시적으로 entropy 에 대한 penalty term 을 추가해준다.

entropy 에 대한 logit 의 gradient 를 계산해보면, NLL 이 평균으로부터 얼마나 떨어져 있는지 deviation 을 가중 평균한 값이 나온다. 아래 식 우변의 가장 끝에 있는 H(p_theta) 에는 i 가 없으므로, 전체 class label 에 고르게 확률값이 분포해있어야 함을 뜻한다.


아래 plot 을 보면, label smoothing 과 ERL(Confidence penalty) 의 predicted probability의 분포가 true 의 경우에 0.4~0.8 정도를 가지는데, dropout 의 경우에는 1에 가까운 값들이 나옴을 알 수 있다. dropout 테크닉이 모델 일반화에 효과적이라고 하지만, calibration에 기여를 못한다는 것에 흥미로웠다. Dropout 이 model parameter 내부에 noise 를 주면서 subset 모델들을 ensemble 하는 효과를 주어서, weight norm 도 줄여줄 수 있다고 기대했는데, 이정도 poorly-calibrated 는 의외이다. 좀 더 분석해보면, dropout 에서도 calibration 에 기여할 수 있는 여지가 있다고 생각한다.

Focal Loss
focal loss 는 아래 공식을 사용하는 loss function 으로 NLL 에 (1-predicted probability) 에 gamma 승수를 weight 한 값을 사용한다. 이에 따라, confident 한 데이터의 경우, 파라미터 업데이트에 작은 기여를 하게 만들어 object detection 과 같이 class imbalance가 일반적인 분야에 효과적인 방법론으로 사용된다.
이러한 focal loss 는 calibration 에도 적합하게 사용될 수 있는데, 그 이유는 NLL 은 predicted probability 가 one hot vector 가 아닌 이상 동일한 중요도로 계속해서 학습이 진행된다. 이 때, focal loss 를 사용하게 되면 confidence 가 높아질 수록 전체 loss 에 끼치는 영향도를 줄임으로써, over-confidence 의 경향성을 효과적으로 막아줄 수 있게 된다. 논문을 읽으면서 개인적으로는 가장 좋은 아이디어라고 생각하였다.
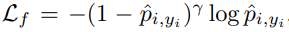
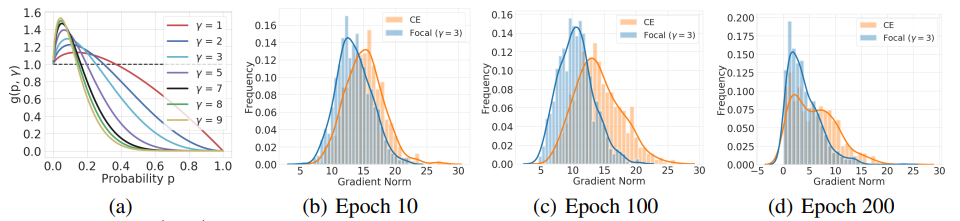
결과부터 보자면, 아래의 plot (a)부터 (d)까지는 은 다양한 모델로 여러 가지 데이터를 실험한 것으로, (b)를 제외하고는 epoch 수가 일정이상 올라가면 diverge 하는 CE (log loss) 와는 달리 계속해서 수렴해가는 focal loss 를 볼 수 있다. 또한 (e) 그래프에서는 CE 가 diverge 할 때, last linear layer 의 weight norm 또한 같이 diverge 하는 것을 볼 수 있다. 이 관계 또한 흥미롭고 동시에 어느정도 예상되는 결과로 focal loss 는 이러한 diverge 를 NLL 앞의 weight term 으로 막아주고 있음을 볼 수 있다.

아래 proposition 을 보면, last fc layer 에 가해지는 gradient 의 focal loss / CE 의 비율을 g(p,gamma) 로 표현하였으며, 해당 값의 변화에 따라, last fc layer 의 vector norm 이 바뀌고, 이는 학습 과정에서 모델의 confidence 를 조정해줄 것이다.

아래 plot 의 (a)를 먼저 보면, 학습 초반 model 이 정답조차 이야기하지 못하는 상황인 경우 (under-confidence 또는 0에 가까운 probability 반환) 높은 g(p, gamma) 를 주면서, CE 보다 더 큰 step 으로 last linear layer 를 학습시킨다. 이후, 모델이 일정 이상 값 (0.2) 을 반환하게 되면, 기하급수적으로 해당 데이터에 대한 gradient 를 줄여줌을 볼 수 있다. 즉, focal loss 는 model calibration 에 기여함과 동시에 학습 초기 빠른 업데이트를 지원함으로써, 빠른 학습을 지원한다.
이에 따른, last linear layer 의 weight norm 을 보면, 전반적으로 focal loss 의 경우가, CE 보다 작게 되며 이러한 경향성은 학습을 계속 해나감에 따라, 두드러진다.
Mix-Up
이전 포스팅에서 언급했듯 두 데이터를 합쳐서, 새로운 x,y pair 를 만드는 mix-up 은 calibration 에 효과적이라고 한다.

아래의 plot을 보면, mixup 이 위에서 다룬 label smoothing 과 ERL 보다, 더 높은 calibration 성능을 vision 영역에서 보이고 있다. (훌륭한 시각화이다...)
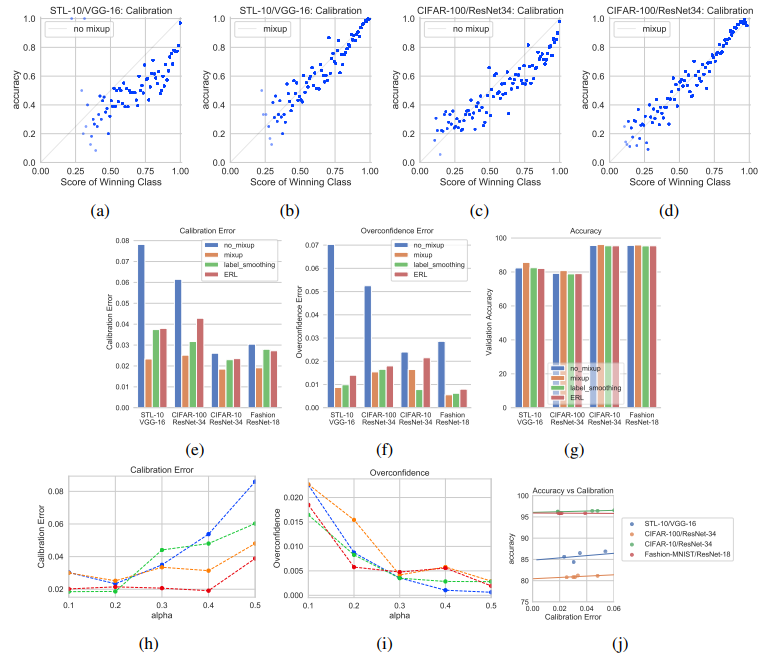
재밌는 실험 중 하나는, mixup 을 feature (hidden layer) 에만 적용하고, class label 은 augmentation 의 형태로 하나만 주었을 때는 calibration 성능이 현격히 떨어짐을 보였다는 것이다. 이로부터, 전반적인 방법론에서 calibration 은 class label 에 대한 전처리가 가장 성능 효과가 큼을 알 수 있다.

Experiments [링크]
1편부터 3편까지 다룬 것들로 실험을 진행하였고 이에 대한 결과를 공유하려 한다. 우선 사용한 모델의 옵션들을 나열해보면 아래와 같다. 참고로 모델 학습은 리소스의 한계로 20 epoch 정도를 진행하였고, 이에 따라 모델이 수렴했다고 이야기할 수 없으며, 결과 해석의 신뢰도에 한계가 있을 것으로 보인다.

아래는 tensorboard 로 시각화한, 각 성능지표들의 batch 별 값들로, hyperparameter tuning 을 하지 않았기 때문에, validation dataset 이지만, test dataset 이라고 보면 된다. 가장 아래 calibration loss plot 을 보면, mix-up 과 focal loss 가 상대적으로 좋은 calibration 성능을 보여주고 있으며, 전반적으로 focal loss 가 우세함을 볼 수 있다.

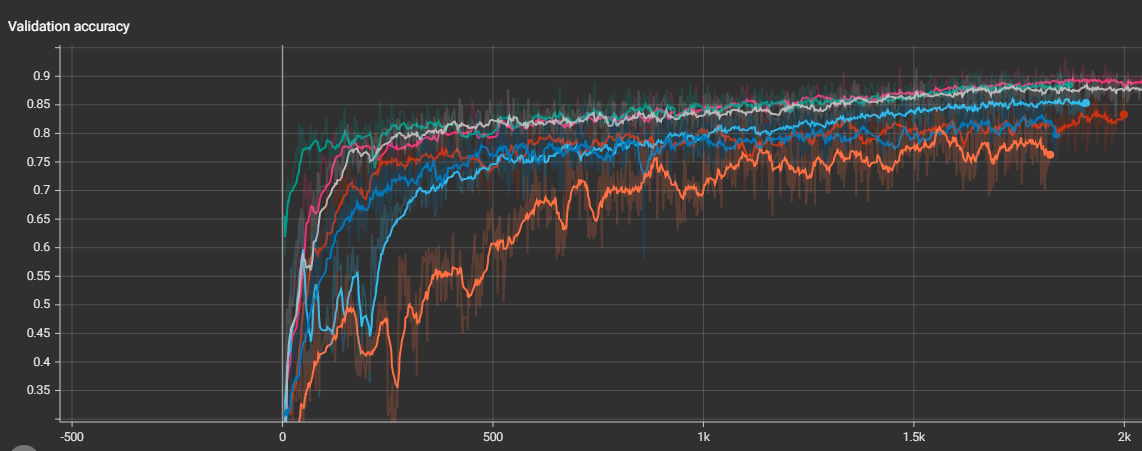
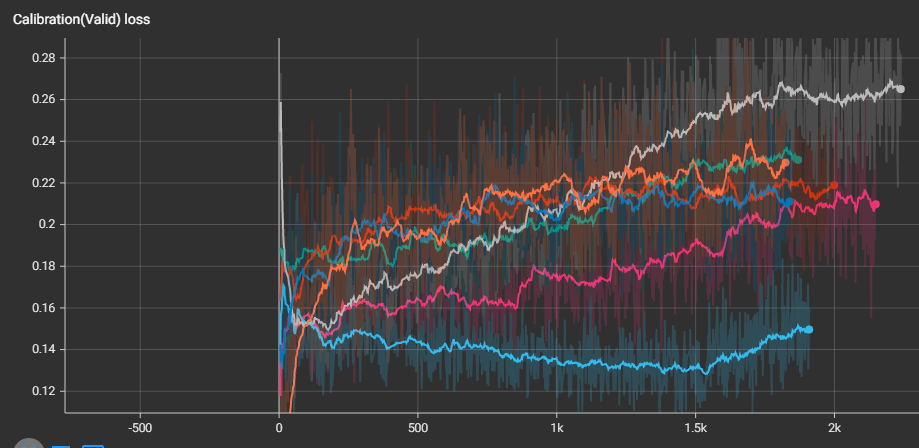

위의 플롯은 predicted probability 를 0.1 단위로 binning 한 classwise-ECE (아래의 범례에서 umean/umax) 만을 보았기에, predicted probability의 분포를 고려한, classwise-ACE (아래의 범례에서 qmean/qmax 를 의미) 함께 보았다. 또한, 2편에서 다룬 sigmoid scaling 을 사용하기 위해, validation dataset 을 사용하였고 이에 따라 아래의 성능 지표는 test dataset 을 통한 것이다.
예상 외의 결과가 나왔는데, 모든 calibration 성능 지표에서 sigmoid scaling 이 우위를 차지하였다. 이에 반해, log loss는 가장 안좋은 값 (가장 높은 값) 이 나왔는데, 이는 모델의 classifiation error 가 가장 높기 때문으로 보인다.
위의 validation dataset 에서 focal loss 사용이 가장 좋게 나왔지만, 아래의 경우에는 mix-up 이 더 우위에 있음을 볼 수 있다. mix-up 의 경우 log-loss 와 accuracy 모두 가장 높은 점수가 나왔고, calibration error 또한 Top-1 인 sigmoid scaling에 크게 뒤지지 않는 Top-2 의 성능을 보여주기 때문에, mix-up 이 결과적으로 가장 매력적인 방법으로 보인다.
Calibration loss 관점에서는, sigmoid re-calibration 방법이 가장 효과적이였지만, log loss 와 accuracy에 대한 과적합 정도가 다른 방법론보다는 높기 때문에, 전반적으로 mix-up 이 가장 효율적으로 보인다.
calibration 에 효과적이라고 불리는 방법론을 사용한 경우 그렇지 않은 경우보다 항상 더 좋은 calibration performance 를 보여준다.
3번의 포스팅을 통해 model calibration 에 대해 알아보았다. 해당 분야는 model uncertainty 과 긴밀하게 연결되어 있어, 해당 분야도 함께 묶어 다룰까 했지만, 너무 방대하고 어려운 분야라 우선 이정도로 끝마치고 나중을 도모하려 한다.
'[간단 정리]' 카테고리의 다른 글
| Karpathy ChatGPT 강의 메모 (0) | 2025.02.09 |
|---|---|
| OpenAI's structured output (0) | 2024.09.11 |
| [간단 정리] model calibration 에 대해 알아보자 (2) (0) | 2021.11.06 |
| [간단 정리] model calibration 에 대해 알아보자 (1) (1) | 2021.11.04 |
| [간단 정리] Neural-Network 는 multi-collinearity 의 영향을 받지 않는가? (0) | 2021.08.19 |


