TechY
[논문 정리] Active Learning Literature Survey 본문
Active Learning을 위해서 한 번은 거치고 가야할 논문, Burr Settles 교수가 쓴 2010 년의 Survey “Active Learning Literature Survey” 에 대해 이야기해보도록 하겠습니다. 본 포스팅에서 나오는 캡쳐 이미지는 모두 해당 논문에 기인한 것입니다.
절차는 다음과 같습니다.
- Active Learning 이 무엇인가?
- Scenarios – Learner 와 Oracle의 관계 프로세스를 정의하는 방법론
- Query Strategy Frameworks – Instance를 query 하는 방법론
절차에 대한 세부 설명에서 익숙치 않은 용어들이 등장하였습니다. 해당 용어들은 Survey 에 자주 나오는 단어들로 이에 대한 정의를 미리 해보도록 하겠습니다.
- L : 라벨 데이터
- U : 라벨이 없는 데이터
- Instance : U 데이터셋의 개별 데이터
- Learner : L 데이터셋을 보고 학습하는 모델 (DNN, SVM etc)
- Oracle : U 데이터셋의 특정 Instance에 대해 라벨링(annotating)을 하는 사람 또는 객체
- Query : U 내에 있는 Instance를 L 데이터셋으로 추가하기 위한 작업
What is Active Learning?

위의 이미지에서, 두 가지 카운터파트가 존재합니다. “라벨 데이터와 언라벨 데이터” 그리고 “모델과 사람” 전자는 기존의 머신 러닝에도 존재하는 개념인데, 문제는 후자입니다. Active Learning이라면 학습을 하는 것일텐데, 왜 사람이 있게 될까요? 사람이 모델을 도와주어 지속적으로 서로 상호작용하며 학습하는 방법론 그것이 바로 “Active Learning”의 기본 아이디어입니다.
일단, 사람이 모델을 도와주어서 문제를 같이 해결해나간다는 것까진 알겠는데, 결국 중요한 것은 “왜?”의 문제겠죠? 아래의 표를 보면서 계속 이야기를 해볼까요?

왼쪽부터 차례대로 이야기를 해보겠습니다. 일단 데이터가 있게 됩니다. 색깔이 두개이니, binary classification 문제라고 하면 되겠네요. 두 번째 plot 을 보면, 각 사이드에 점들이 흩뿌려져 있는 것을 볼 수 있습니다. 이는 U에서 random sampling을 통해 뽑아진 데이터들을 oracle이 라벨링을 한 후, 모델을 트레이닝을 한 것인데요. 논문에 따르면, 70% 의 정확도를 가졌다고 하였습니다. 마지막 plot을 보면, 뭔가 점들이 오밀조밀하게 decision boundary 주변으로 달라붙어서 형성된 것을 느끼실 수 있습니다. 즉, 모델의 decision boundary 를 형성하는데 있어서 영향력이 상대적으로 높고, 유의미한 instance를 선별적으로(selective) 뽑아 이에 대해 oracle이 라벨을 단 것이죠. 이에 대한 결과로 논문에 쓰여진 정확도는 90% 로 이전 plot보다 높은 수치임을 알 수 있습니다.
자, 이제 정리를 해볼까요? 실제 세상에서 라벨이 있는 데이터는 라벨이 없는 데이터보다 훨씬 적습니다. 이에 따라서, 엄청난 성능의 모델이 나오더라도 라벨이 달린 데이터가 없다면 아무 쓸모가 없게 되는 것이죠. 이에 따라 우리는 적은 라벨로도 충분한 라벨 데이터를 가지고 있는 것과 유사한 성능을 보이는 방법론을 생각해야 했습니다. 모델 또는 사람 혼자서는 힘든 작업이였죠. 이에 따라 나온 생각이 바로 “모델이 데이터를 학습하고, 어? 이 데이터는 내가 잘 모르겠어.. 도와줘 주인님!” 이라고 외치면, 주인이 “아 이건 헷갈리만 했네. 이건 사실 어쩌구야!” 라고 이야기해주게 된다면, 모델을 그 피드백을 받아, 계속 성장해 나가고, 결과적으로 모든 데이터에 대해 라벨이 없어도 지도 학습과 유사한 라벨 예측이 가능하게 되는 것입니다. 여기서 중요한 것은 “이걸 모르겠어!” 라고 말하는 부분인데, 아무 데이터에 대해서 라벨을 달아주는 기존 학습 방법과는 달리, 실질적으로 모델의 성능에 기여할 수 있는 데이터에 대해서만 라벨링을 해주면 된다는 맥락이 됩니다.
아직도 이해가 잘 안가신다고요? 아래의 그림을 좀 더 살펴보겠습니다.

위 플롯의 빨간 선은 Active Learning의 방법론 중 하나인 uncertainty sampling 을 한 모델의 learning curve입니다. 보라색 선은 random sampling으로, 모델 학습 과정에서 랜덤으로 라벨이 달린 데이터를 모델에게 학습 시킨 결과가 됩니다. learning curve의 기울기에서 알 수 있다시피, 모델이 학습하는 데에 유용한 데이터만 던져 줌으로써, 적은 라벨 데이터 셋을 필요로 함에도 불구하고, 빠른 학습과 높은 성능을 볼 수 있는 방법론이 바로 “Active Learning”이 되는 것입니다.
Scenarios
Active Learning에서 이야기하는 Scenarios는 Learner 와 Oracle 사이에 datasets 의 흐름에 대한 방법론에 대한 것입니다.

총 세 가지 방법론이 존재하는 데 이에 대해 하나씩 살펴보도록 하겠습니다.
Memebership Query Synthesis
원문을 인용하면 “queries that the learner generates de novo, rather than those sampled from some underlying natural distribution.” 이라는 표현이 나옵니다. 예시로 들어볼까요?
Learner : “이런 데이터는 라벨을 매기기가 너무 애매해..중간 즈음에 있는 데이터 [-0.1,-0.54, 0.13, 0.35 … ] 는 어떤 것 같아?”

즉, 쿼리를 보낼 때, 실제로 가지고 있는 데이터에서 샘플링해서 보내는 것이 아니라, Leaner 가 input space에서 생성한 (generates de novo) 데이터를 쿼리로 보내서 Oracle에게 라벨링을 요청하는 구조가 됩니다.
언뜻보면, 그럴 듯 해보이는 데 어떤 문제가 있을까요? 예로 들어 handwritten character를 image classification하는 문제를 풀고 있다고 해봅시다. 모델이 특정 포인트를 잡아서 쿼리를 보내서 우리가 봤는데, 이건 대체 알아볼 수가 없는 글자가 되고 마는 것이죠. 즉, oracle이 human annotator여서, 사람이 이를 해석하고 라벨링을 달아주어야 하는 경우에 문제가 생긴다는 단점이 있습니다.
Stream-Based Selective Sampling
원문을 인용하면 “each unlabeled instance is typically drawn one at a time from the data source, and the learner must decide whether to query or discard it.” 이라는 표현이 나옵니다. 예시로 들어볼까요?
유희왕 : 마법카드 발동! 이 마법카드는 한 장을 드로우해서 공격력이(정보력이) 1000보다(정보력의 하한선) 높은 카드(데이터)일 경우, 필드 위에 발동할 수 있고 (쿼리할 수 있고) 아니면, 묘지로 보낸다!(그냥 지나친다)
못난 예시 죄송합니다… 파이썬 코드 예시로 한 번 살펴보도록 하겠습니다.
informative_treshold = 0.5 for instance in unlabeled_data : instance_inform : query_strategy(instance) if informative_treshold > instance_inform : print("query!") else : print('discard!')
인스턴스를 하나씩 뽑아서 순차적으로 확인하고 정보력에 따라 쿼리 여부를 결정하는 방법론이 되겠습니다.
Pool-Based Sampling
논문을 인용해보면, “evaluates and ranks the entire collection before selecting the best query.” 라고 표현이 되어 있습니다. 이 또한 예시로 살펴보겠습니다.

Learner : “가만 보자.. 제일 정보력이 높은 거 2개를 고르기로 했으니까, Data1 , Data2 를 쿼리하면 되겠다!”
이전의 방법론과 차이점이 느껴지시나요? Steam-base 와 Pool-base의 차이점은 전자는 sequentially 하게 개별 데이터의 정보량을 파악해 쿼리하는 것이고, Pool-base는 데이터를 모아서 pool로 보고, 이 중 정보력있는 k개를 쿼리하는 것이 됩니다!
Query Strategy Frameworks
Scenarios 에서 저희는, Learner 가 적은 양의 L을 통해 학습, U를 예측하는 과정에서 informative 한 instance를 쿼리하는 일련의 구조를 살펴보았습니다. 그 다음으로 이야기하는 Query Strategy 에서는 특정 instance에 대해 얼마나 정보력이 있는지를 계산(measure)하는 다양한 방법론에 대한 이야기를 하게 됩니다.
- Uncertainty sampling
- Least Certain
- Margin Sampling
- Entropy Sampling
- Query-By-Committee
- Exspected Model Change
- Expected Error Reduction
- Variance Reduction
- Density-Weighted Methods
Uncertainty Sampling
본문을 인용하면 “an active learner queries the instances about which it is least certain how to label. – nearest 0.5” 의 표현이 나오게 되는데, 가장 “불확실한” 인스턴스를 뽑아서 쿼리하는 것의 맥락이 됩니다.
- Least Certain

softmax 값이 [0.2, 0.3 ,0.5] 가 하나 있고, [0.1, 0.2 ,0.7] 이 나온 두 개의 인스턴스가 있다고 하면, 각각의 y_hat 이 0.5, 0.7 이기 때문에, 더 uncertain 한 것은 첫 번째 instance 가 됩니다. 참 쉽죠?!
- Margin Sampling

margin sampling
위의 예시의 경우, 각각의 margin 값은 0.5-0.3 = 0.2, 0.7 - 0.2 = 0.5 이에 따라 더 uncertain 한 것은 첫 번째 instance 가 됩니다. 즉, 최종 결정이 얼마나 두드러지고 경쟁력있게 이뤄지냐에 대한 문제입니다.
- Entropy
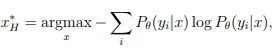
entropy
엔트로피는 분포의 불확실성을 계산하는 대표적 단위로 고르게 이뤄진 ls1 이 더 높은 정보력을 가지고 있는 것을 확인할 수 있습니다.

Uncertainty Sampling 방법론들은 저마다의 특징이 있고, 이에 따라 다른 특성들을 가지게 됩니다. 대표적으로, entropy 방법은 하나의 라벨에 대한 probability space가 유난히 작을 경우, informative score가 낮아지고, 반면에 LC 와 margin sampling은 그 값이 높아지게 됩니다. 예시를 들어보면 아래와 같습니다.
ls1 = [0.01, 0.3, 0.79]; ls2 = [0.1,0.2,0.7] print('entropy : ',entropy(ls1),entropy(ls2)) print('LC : ',LC(ls1),LC(ls2)) print('Margin : ',Margin(ls1),Margin(ls2)) entropy : 0.87 , 1.16 LC : 0.21 , 0.30 Margin : 0.49 , 0.50
위를 보면, ls1이나 ls2이나 둘 다 비슷해보이는데, ls1의 정보력이 훨씬 낮은 수치를 보입니다. 왜일까요? 그 이유는 ls1의 0번째 라벨 예측 값이 매우 낮은 확률 형태를 보이게 되고, 이에 따라 해당 인스턴스는 0번째 라벨은 아닐 것이다. 라는 나름의 확신을 가지게 되기 때문에, 정보력을 잃게 되는 것입니다.
추가적으로는, entropy 방법의 경우 log-loss를 최소화하는 문제에 적합하고, LC와 margin sampling의 경우, classification error를 최소화하는 문제에 적합하다고 합니다. Q. 그렇다면 NLLLoss 를 사용하는 Classification의 경우에는 어떻게 될까요? 실험을 해봐야 알 문제일 것 같네요.
Query-By-Committee
사공이 많으면 배가 산으로 가지만, 사공이 저밖에 없으면 그냥 바다 위에 동동 떠있게 될 수도 있겠죠? 여러 모델들이 특정 인스턴스에 내린 다양한 결정들을 보고, 이에 따라 정보력을 계산해 쿼리하는 방법론을 QBC Approach 라고 합니다.
모델은 같은 데이터 LL을 학습했지만 다른 모델로 다른 학습 파라미터 θθ 를 가지게 됩니다.
C={θ1,θ2,...,θC}C={θ1,θ2,...,θC}
- Vote Entropy
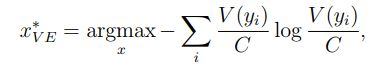
위의 등식에서 V(yi)V(yi) 가 의미하는 것은 i번째 라벨에 대해서, 옳소! 라고 외친 Committee의 수를 의미합니다. 예로 들어서 “나는 너무 행복해” 라는 문장에 대해 5개의 Committee 중 4개의 모델이 “이것은 긍정이오!” 라고 외친다면, V(yi)V(yi)가 될 것이고, CC로 나눠줌에 따라, ratio 또는 확률의 형태가 됩니다. 이후로는 uncertainty sampling의 entropy approach 와 동일합니다.
- Kullback-Leibler (KL) divergence

KL divergence는 두 분포의 차이(거리)를 정량화하는 방법론으로, 위의 식에서 분자가 의미하는 것은 cc번째 Committee 가 ii번째 인스턴스에 내린 결정이 됩니다. 예로 들어 [0.7,0.2,0.1]이고 ii가 0이면 0.7이 되는 것이죠. 아래의 분모 분모는 ii 번째 인스턴스에 대한 전체 Committee의 결정이 됩니다. 결과적으로 해당 KL divergence 가 구하고자 하는 것은 전체의 의견과 개별 committee의 의견이 얼마나 많이 분산되어 있느냐에 대한 문제이고, 모델마다 예측에 대한 분포 차이가 너무 크면 정보력이 높은 것이다라고 간주하게 되는 것이죠.
Expected Model Change
“어렸을 때, 이걸 알았다면 내 인생이 정말 많이 달라졌을텐데..” 라는 말 들어보신 적 있으신가요? 이와 같은 생각을 방법론을 끌어온다면 다음과 같게 됩니다. “이 인스턴스에 대한 라벨을 알았다면, 내 모델은 정말 많이 달라졌을텐데..”
몹쓸 예시를 뒤로 하고, 해당 방법론에 대해 말씀드리면, ‘모델을 가장 많이 변화시킬 수 있는 인스턴스를 쿼리한다!’ 가 주요 아이디어가 됩니다. 모델의 변화도는 Gradient 로 계산할 수 있게 되고, 공식은 아래와 같습니다.

우변의 Euclidean distance 가 씌워진 부분이 바로 모델이 얼마나 변화하였는지를 정량화하는 부분인데, 소괄호 안의 표시는 기존의 라벨 데이터 LL에서 ii번째 라벨이 달린 xx 인스턴스가 추가되었을 때를 의미합니다. 저희는 특정 인스턴스의 실제 라벨을 oracle이 달기 전까지는 알지 못하기 때문에, 각 인스턴스가 가질 수 있는 모든 라벨의 경우의 수에 대한 gradient 값을 Euclidean distance로 값을 변환해 이를 더해준 것을 기댓값으로 사용합니다.
해당 방법론의 흥미로운 점을 하나 더 말씀드리면, 소괄호 안의 LL이 없어질 수 있다는 것입니다. 기존의 라벨 데이터를 가지고 학습시킨 learner 는 LL에 대한 gradient 변화가 0에 가까울 것이기 때문에, LL와 새로운 인스턴스를 합집합한 것에 대한 gradient 를 계산하는 것이 아닌, 새로운 인스턴스에 대한 gradient 변화값만 측정하여, 근사를 취하기 때문에 연산 효율성을 꾀할 수 있게 됩니다.
Expected Error Reduction
이전의 방법론은 특정 인스턴스가 모델을 얼마나 변화시킬 지에 집중했다면, 해당 방법론은 해당 인스턴스를 사용함으로써, 모델의 에러가 얼마나 감소할 지에 집중합니다. 보다 구체적으로 말씀드리자면, UU 에서 특정 인스턴스를 쿼리한 후, re-training 한 모델이 그 인스턴스를 제외하고 남은 UU에 대해 예측을 해보았을 때, 최대한 에러가 적어야 한다는 것입니다. 즉, “validation dataset을 잘 맞출 수 있게 하는 validation data를 찾아라!” 가 됩니다.
-
0,1 loss 의 경우,

-
log loss 의 경우,

Variance Reduction
모델의 에러를 줄이거나, gradient 를 계산하는 것들은 연산 비용이 높고, 닫힌 해가 아니게 될 수 있다는 문제점이 있습니다. 이에 따라 모델의 variance 를 줄일 수 있는 인스턴스를 찾아보자! 라는 시도가 생겨나게 됩니다.
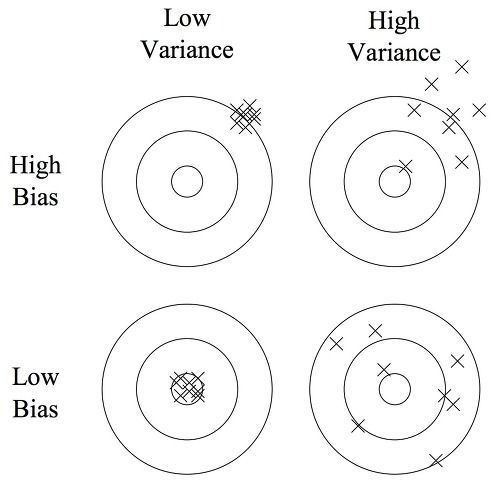
예측 모델의 에러는 분해되어 설명될 수 있습니다.
- Error(X) = noise(X) + bias(X) + variance(X)
- noise 는 데이터가 가지는 본질적인 한계치 – irreducible
- Bias 는 모델이 잘 못맞추는 것이다. 모델이 별로거나, 데이터가 적거나의 문제. (underfitting) – irreducible
- Variance 너무 잘 맞추려다 보니, 그것만 잘 맞추게 되는 민감도의 문제. (overfitting) – reducible
Variance를 줄이기 위한 노력은 딥러닝에서 Dropout, Regularization 등 많은 방법론을 통해 시도되어 오고 있습니다. 즉, 해당 모델을 사용하는 유저가 특정 프로세스를 통해 오버피팅을 방지하는 과정에서 모델의 variance를 줄일 수 있게 된다는 것이죠. 해당 방법론 또한 모델이 뱉어내는 결과값 자체의 분산을 줄여주는 인스턴스를 쿼리하는 방법론에 대해 이야기합니다.
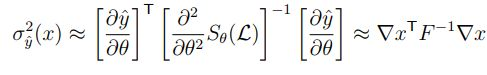
위의 공식은 뉴럴 네트워크 결과값의 분산에 대한 근사식입니다. – MacKay (1992) 양 옆에는 모델 파라미터에 따른 출력값의 변화도, 즉 저희가 흔히 알고 있는, gradient 입니다. 그렇다면 가운데 FF는 대체 무엇을까요? 바로 Fisher information matrix라고 불리는 output log probability의 covariance를 의미하는 부분입니다. 보시다시피, F−1F−1 로 inverse 가 취해져 있어서, 출력값의 분산을 줄이기 위해서는 output의 covariance인 Fisher information matrix를 극대화해야 한다는 결론이 도출됩니다.
수식을 떠나 이야기를 해보면, Fisher information matrix는 모델이 얼마나 불확실한지를 측정하는 도구이고, 해당 값이 높을 수록 모델의 uncertainty는 높아지게 됩니다. 그 이유는, 이 자체가 log probability의 공분산을 의미하기 때문이죠. 저희가 원하는 것은 모델의 variance가 줄어들게 해주는 인스턴스입니다. 그렇다면 모델의 분산을 높게 만드는 인스턴스에 대해 라벨링을 해주어서 확실하게 바꿔준다면, 모델의 분산은 크게 작아지게 되겠죠.
추가적으로, 이상적인 경우, loss function 은 convex 하기 때문에, gradient of x 는 locally linear 하고, variance 형태인 F는 Gaussian 을 따르게 되기 때문에, Closed form 이 된다고 합니다.
Density-Weighted Methods

위의 사진에서 색깔이 있는 점은 라벨 데이터이고, 동그란 점들(UU) 중, 인스턴스를 선택해 쿼리해야 합니다. 가장 불확실한 것은 무엇일까요? 바로, decision boundary 위에 떡하니 올라와 있는 AA 가 됩니다. 하지만, 과연 AA 가 전체 UU 를 대표할 수 있을까요? outlier 처럼 보이는데 말이죠..흠.. 이러한 문제에 따라, 다른 UU와 얼마나 군집해있냐에 대한 부분을 추가적으로 고려하여 인스턴스를 선택하는 방법론이 되겠습니다.

우변의 첫 번째 식은 저희가 이전에 보았던 다른 query strategy입니다. 중요한 것은 소괄호 안에 있는 것인데요, sim(x,x(u))sim(x,x(u)) 를 취해줌으로써, 선택하려는 인스턴스와 나머지 UU간의 similarity 즉, density를 계산해 가중치를 부여하는 방식이 되겠습니다.
'[논문 정리]' 카테고리의 다른 글
| [논문 정리] A STRUCTURED SELF-ATTENTIVE SENTENCE EMBEDDING (0) | 2020.12.15 |
|---|---|
| [논문 정리] Unsupervised Deep Embedding for Clustering Analysis (0) | 2020.12.15 |
| [논문 정리] A simple method for domain adaptation of sentence embeddings (0) | 2020.12.12 |
| [논문 정리] Training Temporal Word Embeddings with a Compass (0) | 2020.12.08 |
| [논문 정리] Diverse mini-batch Active Learning (1) | 2020.11.28 |




