TechY
[논문 정리] DEEP TEMPORAL CLUSTERING: FULLY UNSUPERVISED LEARNING OF TIME-DOMAIN FEATURES 본문
[논문 정리] DEEP TEMPORAL CLUSTERING: FULLY UNSUPERVISED LEARNING OF TIME-DOMAIN FEATURES
hskimim 2021. 7. 19. 03:23딥러닝 기반의 time-series clustering 논문을 리뷰해보려 한다. 혹시 DEC 논문을 읽은 사람이라면, 가볍게 훑으면 다 읽을 수 있을 정도로 거의 유사한 아키텍처를 가지고 있다. 참고한 소스 코드는 해당 깃헙을 참고하였다.
1. Architecture
제시된 모델의 아키텍처는 아래 이미지와 같으며, 크게 두 개의 서브 아키텍처와 이에 해당되는 loss 로 구분 가능하다.
1. Temporal Auto Encoder : Reconstruction Loss
2. Clustering Net : KL divergence loss

1.1 Temporal Auto Encoder
이부분은 간단하며, 크게 어려운 부분이 없다. spatio-temporal 한 특징을 잡기 위해, Convolution 연산 후, bi-LSTM 을 적용해 encoding 을 했으며, decode 부분에서는 Upsampling 후 decovolution 을 적용해주었다. 대칭적으로 해주지 않은 것에 대한 이유는 언급되지 않았다. 이런 reconstruction architecture 는 선행 연구에 따른 것일 수도 있겠다. (무엇이 되었든 좀 써주었으면 좋았을 듯 하다...)
2.2 Clustering Net
해당 아키텍처는 1.1 의 TAE 모델과 독립적이지 않은 end-to-end network 로 TAE 모델의 encoder 가 만든 latent vector z_i (i 는 데이터 하나를 의미) 를 인풋으로 받는다. z_i 는 모델 내에서 초기화된 centroid vector w_j (j는 cluster 하나를 의미) 와 siml 이라는 measure 를 통해, 유사도가 계산된다. 이 때 사용되는 similarity measure는 논문에서는 다양하게 제시하는데, 결과적으로는 Complexity Invariant Similarity (CID) 라는 measure 의 성능이 상대적으로 가장 좋았다.
논문에서 centroid vector w_j 를 찾는 과정은 DEC 논문의 방식과 동일하며, 이는 dimensionality reduction 을 통한 시각화를 지원하는 알고리즘인 t-SNE 를 따른다. TAE 모델이 input sequence 를 차원 축소한 형태이고, 이렇게 축소된 벡터들과 centroid vector가, raw sequence 들과 우리가 모르는 true centroid vector 간 similarity 를 잘 보존하게끔 조정되어야 하기 때문에, 적합한 목적 함수를 갖출 수 있다.
첫 번째, q는 latent vector z_i 와 centroid vector w_j 간의 similarity 이다. 분모 부분의 normalize 과정을 통해 확률값의 형태로 표현된다. 즉, z_i 가 w_j cluster 에 속할 확률을 나타낸다. alpha 값은 student t-분포의 degree of freedom 을 나타내며, TSNE 의 저자가 제안한 바에 따라, (alpha=1 이 unsupervised setting 에서 좋다) alpha 를 1로 하였다.

원래 t-SNE 에서 p 는 encode 되기 전, raw vector 의 실제 거리를 의미한다. 즉, 정답 distance measure 를 의미하는데, unsupervised setting 에서는 실제 p 를 알 수 없다. (clustering task 이기 때문에, 정답 centroid vector 가 없기 때문이다.) 저자가 사용한 p_ij 는 아래와 같은데, 이 또한 DEC 논문과 같다. 위에서 계산한 q 값에 square 를 취해주고 이 값을 모든 데이터에 대한 q 로 나눠준 값을 사용한다. 그리고 q 와 마찬가지로, 확률값으로 만들어준다.


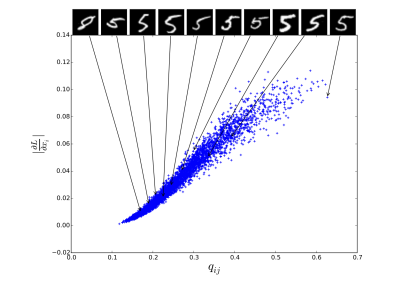
이러한 p 를 사용한 이유에 대해서, DEC 논문에서는 auto-encoder 가 high confidence 로 예측한 값들이 대부분 옳을 것이다라고 가정한 결과이다. 아래의 이미지는 DEC 논문에서 가져온 것인데, 첫 번째로는, cluster centroid 에 가까울 수록, 더 높은 gradient 값을 가진다고 이야기 했다. 여기서 gradient 의 magnitude 는 KL divegence 상에서 confidence 의 척도라고 이야기할 수 있다. 이에 따라, 높은 q 값을 믿고 이에 대해 square 값을 취해준 것으로 보인다.
높은 q 값을 신뢰하기 위해, auto-encoder pretraining 과 centroid vector initialization 이 중요하게 여겨지고, end-to-end learning 전에 TAE 부분을 따로 pre-training 시키며, cetroid vector w_j 는 초반에 주어진, q들을 agglomerative hierachical clustering algorithm 의 centroid vector 로 intialize 해준다.
이렇게 나온 p 값과 q 값은 확률값의 형태를 가지고 이를 KL divergence로 두 분포를 가깝게 위치하도록 학습시킨다.
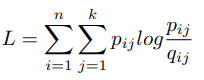
3. Conclusion
전반적으로 저번에 읽은 DEC 논문과 유사해 편하게 읽을 수 있는 논문이었다. 한번 학습시켜봐서 k-shape 과 성능 비교를 해보는 것도 재밌을 듯 하다.
'[논문 정리]' 카테고리의 다른 글
| The Kelly Criterion and the Stock Market (0) | 2024.05.26 |
|---|---|
| [논문 정리] HEAD2TOE: UTILIZING INTERMEDIATE REPRESENTATIONS FOR BETTER TRANSFER LEARNING (0) | 2022.01.19 |
| [논문 정리] k-Shape: Efficient and Accurate Clustering of Time Series (1) | 2021.07.18 |
| [논문 정리] Translation in Multi-modal Learning 논문 정리 (0) | 2021.06.23 |
| [논문 정리] mixup: BEYOND EMPIRICAL RISK MINIMIZATION (0) | 2021.06.11 |




