TechY
[논문 정리] mixup: BEYOND EMPIRICAL RISK MINIMIZATION 본문
제목이 멋있어서, 읽었지만, 유명한 augmentation 기법을 다룬 논문인, mix-up 에 대해 이야기해보겠다. 본 논문과 함께 참고하고 다룰 논문은 아래 두 논문이다.
Augmenting Data with Mixup for Sentence Classification: An Empirical Study
On Mixup Training: Improved Calibration and Predictive Uncertainty for Deep Neural Networks
논문은 초반에 empirical risk minimization(ERM) 과 vicinal risk minimization(VRM) 에 대해 이야기한다. 우선, ERM 에 대해 이야기해보자면, 컨셉은 간단하다.
"우리가 경험한 것에 따라 기대되는 위험을 최소화하자"
뭔가 제목을 풀어쓴 것 같은 느낌이다. 좀 더 수식적으로 보면 아래와 같다.
우선, random feature vector x, 와 random target vector y 를 두고 이 둘의 joint distribution P(x,y) 가 있다고 하자. 쉽게 말하면, 입력-정답 쌍이 있는 데이터의 모집단 분포이다. x-y 관계를 학습하는 함수 f 를 통해 나온 예측값과 실제 y 간 차이에 대해 penalty 를 주는 loss 를 두고 이에 대한 기댓값을 계산하면 expected risk 가 된다.

언제나 늘 그렇듯 우리는 모집단을 모르며 근사할 만한 무언가가 필요하다. 이에 따라, 우리가 모델 f 를 학습시킬 때 사용하는 training dataset 을 통해 분포를 형성하며 이를 empirical distribution 이라고 한다. 즉, 가용한 데이터로 모집단을 근사한다. 많을 수록 근사가 잘 될 확률이 높다.

위의 epected risk 식에서 적분 항 안에 들어가는 probability P(x,y)를 근사시킨 empirical distribution 으로 바꾸면 아래와 같다.

해당 논문의 주장에 따르면, ERM 을 통한 모델 학습은 n (위의 식에 따르면, # of empirical data 를 의미) 개의 finite set 만이 학습에 가용하며, 딥러닝과 같이 파라미터가 많은 모델을 학습할 경우, empirical distribution 을 전부 외워버리는 문제가 발생할 수 있다고 한다.
이렇게 제시되는 것이, VRM 이다. 우선 vicinal, vicinity 는 "부근의", "근접의" 라는 뜻으로써, vicinal distrbitution 은 우리가 가지고 있는, 데이터 쌍 x,y 에 근접한 다른 데이터 쌍 x', y' 들의 분포를 의미한다. 이러한 분포에서 샘플링된 데이터로 expected risk 를 최소화하게 되면, empriical vicinal risk 를 다룬다고 이야기한다.

VRM 을 처음 제안한 논문에서는, gaussian vicinity 를 제안했는데, 이는 원 데이터 쌍과 떨어져 있는 정도(거리)가 normal distribution 에서 나왔음을 이야기한다. 그리고 이는 target vector y 는 동일하게 부여하되, random feature vector x 에 gaussian noise 를 더한 것과 동치라고 한다. 이렇게, VRM 을 사용하면 empirical data 보다 많은 양의 데이터를 사용할 수 있게 되고 augmentation 의 관점에서 볼 수 있게 돈다.
저자는 vicinal distribution을 일반화한 식을 제시했는데, 근접한 정도에 대한 분포를 beta distribution 으로 하며, 가지고 있는 emprical distribution 에서 어디쯤에 위치하고 있는 지를 lambda 값으로 조정하면서 결정하는 형태로 보인다. lambda 값은 Beta(a,a) 를 따르는 distribution 이다.


일반화 식은 우리가 가지고 있는 모든 데이터셋을 통해 vicinity 를 구하지만, 쉽게는 아래와 같이 2쌍의 (x,y) 로 vicinal distribution 을 생성할 수 있다.

What is mixup doing?
저자의 주장에 따르면, mixup 은 모델이 training data 간에 선형적인 양상 (linear behavior) 을 가지게끔 해준다고 한다. 이 linear behaviour 는 out-sample 에서 예상치 못한 결과물 (undesirable oscillations) 을 내뱉는 것을 줄여줄 수 있다고 하며, overfitting 을 완화시켜주는 장치로도 사용될 수 있으며, 적대적 데이터에도 강건함을 가질 수 있게 도운다.

+ Improved calibration
mixup 이 calibration 의 관점에서도 성능 향상을 보인다는 연구 또한 존재한다. calibration 이란 모델이 예측에 대해 확신하는 정도와 예측이 맞을 확률의 관계에 대한 것으로, DNN 모델의 over-confident 한 문제를 다루기 위해 calibration을 향상시키려 한다.

위의 이미지를 보면, mixup 과 함께 비교군으로 "epsilon smoothing label" 기법과, "entropy-regularized loss(ERL)" 기법을 가지고 실험을 한 결과이다. 논문에서, Expected Calibration Error (ECE) 와 Overconfidence Error (OE) 에 대한 measure 를 제시하였고, 이를 시각화하였고, 해당 measure 들은 모두, 결국 모델의 confidence (sampling 된 input x 에 대한 예측값(softmax)의 max value들의 평균)과 모델의 accuracy 간의 관계를 보는 것이다.

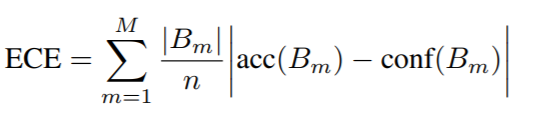

전반적으로 mixup 이 비교군에 비해 잘하고 있는 양상을 보이며, 인상적인 것은 아무것도 하지 않은 경우, 분명한 over-confidence 양상을 보인다는 것이다. 즉, 어떤 방식이든 calibration 을 향상시킬 수 있는 기법을 적용하는 것이 중요해보인다.
또 하나, 재밌던 것은, 자연어처리에 대한 mix-up 이다. calibration을 다룬 논문에서는 자연어 데이터에 대해서도 실험을 진행하였는데, raw data 가 아닌, embedding data 에 대해서 하였다. 이유는, 자연어 데이터는 이미지에서 하는 pixel-mixing 과 같은 방식이 불명확하며, 기본적으로 sequential 하기에, raw data 의 mix-up 이 용이하지 않기 때문이다.

NLP에서 mix-up 을 제시한 논문에 따르면, 위와 같이 두 가지로 나뉘어지는데, 각각 wordMixup 과 senMixup 이라고 부른다. mix-up 을 어느 단계에서 진행하냐의 차이가 존재하고 embedding 을 mix 하는 컨셉은 동일하다. 두 모델 모두 벤치마크 모델을 상회하는 Accuracy 를 보여주었지만, 개인적으로 wordMixup 이 잘되는 건 좀 신기해보인다.
wordMixup의 경우, 문장을 하나의 벡터가 아닌 zero-padded 된 word vector 들의 concat 형태로 가지고 있고, 이를 mix-up 한 후 학습하는 형태인데, sequential data인 자연어 데이터가 품사도 다르고, 길이도 다른 두 문장을 word level 에서 mix-up 하는 것이 과연 real-world data 에서도 잘 될지 의문이다. (직접 해보는 것이 답이다.)
Conclusion
간단한 방법으로 모델의 over-confident 와 regularization 을 효과적으로 할 수 있는 기법이다.
무엇보다, 위에서 보던 것과 같이 어떠한 것이든 기법을 사용하기 전후의 calibration 성능의 차이가 큰 것으로 보아, 꼭 고려해야 할 calibration 기법들 중 매력적인 방법이라고 생각한다.
'[논문 정리]' 카테고리의 다른 글
| [논문 정리] k-Shape: Efficient and Accurate Clustering of Time Series (1) | 2021.07.18 |
|---|---|
| [논문 정리] Translation in Multi-modal Learning 논문 정리 (0) | 2021.06.23 |
| [논문 정리] Deep Metric Learning: A Survey (3) | 2021.06.09 |
| [논문 정리] Learning both Weights and Connections for Efficient Neural Networks (0) | 2021.06.01 |
| [논문 정리] Intriguing properties of neural networks (0) | 2021.02.22 |




