TechY
[논문 정리] Deep Metric Learning: A Survey 본문
어떤 분야를 공부하려고 마음을 먹으면, 어떤 논문을 어떤 순서로 읽어야 할지, 아득해지곤 한다. 이럴 때 가장 좋은 방법은 survey 논문을 읽는 것이라는 이야기가 있길래 시도해보았는데, 엄청난 노력의 산물을 맞닥뜨리니 너무나도 감사하게 잘 읽었다. 앞으로 survey 를 쭉 훑는 포스팅을 해봐도 재밌을 것 같은데..
거두절미하고, 최근 metric learning 에 관심이 생기기 시작했다. 그 이유로는, classification/regression task 가 아닌 특정 task 에 잘 fitting 된 임베딩을 얻을 일이 생겨, 간단하게 코드 구현을 했는데, 학습과 결과가 마음에 들었기 때문이다. 결과를 보고 공부를 시작하는게 좀 이상해보이긴 하지만, 이제라도 좀 알고 써보려 한다.

Metric Learning 은 input data 간 거리를 학습하는 것을 의미한다. 즉, input data 가 존재하고, 이 둘 간의 거리/유사도 를 알고 있다면, 이를 맞추어나가는 과정을 통해, input data를 잘 설명하는 임베딩을 학습하는 것이다. 예로 들어서, CIFAR-10 데이터가 있다고 하면, 모델을 통해 이미지를 한 쌍을 vector 로 임베딩시킨 후, 같은 라벨끼리는 유사도가 높고, 이에 따른 거리가 짧으니, (distance 와 similarity 는 opposite 한 개념이기 때문) 두 임베딩 벡터의 코사인 유사도가 1이 되게끔 모델을 업데이트하고 반대의 경우 0이 되게끔 업데이트하는 방식이다.
유사도를 통해, 임베딩을 학습하는 과정은, 데이터 간 유사도를 파악하는 과정이, input data 를 잘 이해하는 것이라는 가정이 존재하는 것이며, 딥러닝 모델 학습의 목적이, 데이터 간 유사도를 파악하는 경우가 많고, 이를 직접적으로 학습시키는 방법은 효과적이라고 생각한다.
그렇다면, 왜 꼭 metric learning 방식이여야 할까. 사실 꼭 그렇지는 않다. cross-entropy loss 등을 이용한 classification task 를 통해서도, 주어진 라벨을 잘 설명하는, 동시에 각 label 별로 클러스터가 형성되어 있는 임베딩을 얻을 수 있다. (마지막 full-connected layer 를 제거하고 t-sne 를 통해 시각화해서 볼 수 있다.) 하지만, classification task 는 imbalance dataset 에 취약한 특성을 가지고 있다. P(C|X) 를 bayes rule 을 통해서 보면, 분자에 prior 로 P(C) 가 존재하는데, label imbalance 한 경우, 특성 P(C) 가 상대적으로 낮게 되어, 적은 label 값에 대한 예측값을 잘 뱉어주지 않을 뿐만 아니라, 학습 횟수가 낮아, 예측의 신뢰도가 떨어지게 된다.
Metric Learning 은 이러한 문제를 효과적으로 잘 처리해내는데, 그 이유는 간단하다. Classification task 의 경우 우리가 모델에게 알려주는 것은 "input data X는 y 이다" 라는 것이다. Metric Learning 의 경우에는 조금 다른데, "input data X_1은 X_2 와는 비슷하고, X_3 와는 다르다." 이다. 즉, 모델에게 알려주는 정보가 갯수로 하나가 더 많다는 것이다. 이에 따라, imbalanced data 의 경우, positively similar 한 데이터의 pair 는 부족하겠지만, negatively similar 한 데이터 pair 가 매우 많이 존재할 것이고, 이에 따라, 적은 라벨의 데이터는 나머지들과 멀리 떨어지게 되고, 이는 우리가 목표한 바를 최소 절반정도는 이룬 것이다. 하지만, 상대적으로 적은 라벨 데이터 X 끼리 결집되어 있기를 기대하기는 어려울 것 같으며, 이는 리서치해볼만한 주제이다.
Metric Learning 을 하는 과정은 크게 3 가지로 나눌 수 있다. 논문의 표현을 빌리자면 아래와 같다.
1. informative input samples
2. structure of the network model
3. metric loss function
1. informative input samples
즉, positive "or" negative sample 을 뽑는 과정을 의미한다. "or" 라고 쓴 이유는, 특정 loss function의 경우, positive 와 negative 중 하나만 사용하여 학습을 하는 경우가 존재하기 때문이다. 또한, 유사도는 어떤 데이터 하나를 기준으로 두고 정하게 되는데 (ex. ~와 유사한, ~와 유사하지 않은) 이 기준이 되는 데이터는 anchor 라고 한다.
하나의 데이터 셋 X_anchor 에 대해서 이에 응하는 X_positive, X_negative 를 뽑아야 한다고 해보자. (이를 triplet mining 이라고 한다.) 어떤 방법이 있을 수 있을까. 가장 쉬운 방법은 random sampling 이다. 실제로 sampling에 편향이 없기 때문에, 나쁜 방법은 아니라고 생각이 든다. 하지만, 이전 연구에 따르면, 이미 모델이 잘 맞추고 있는 positive/negative pair 에 대해서 (easy pair 라고 한다.) sampling 을 진행하는 것은 학습에 효과가 미비하며, 오히려 test-time 에 역효과를 낳았다고 한다. 또한, positive sample 보다 더 anchor 과 가까이 있는 경우, false-positive 의 가능성이 존재하고, 또한 negative 를 많이 밀어내야 하기 때문에, high variance gradient와 low signal to the noise ratio 가 발생한다고 한다. 내 생각에는, pre-trained embedding 이 아닌 경우, 학습 초반에 이런 경향성이 많이 나올 것으로 예상되는데, learning from scratch 의 경우에 학습 커리큘럼이 어떻게 되는지 이전 연구를 조사해봐야겠다. 또한 커리큘럼 학습 (curriculum learning) 의 특성이 사용될 여지가 있어보이므로, 그것도 조사해보자

triplet mining 에서 많이 사용되는 sampling 기법이 semi-hard sampling 으로 위의 수식을 보면 알 수 있듯, positive sample 보다 anchor 와 멀리 떨어져 있어, 아예 틀린 건 아니지만, positive margin 반경 아래에 있어, 좀 더 분명한 분별이 필요한 경우이다. 이 경우, false-positive 의 경우를 줄이면서, 안정적/효과적으로 학습할 수 있게 된다.
2. structure of the network model
model network 는 크게 Siamese network 와 Triplet network 로 나눌 수 있다. 해당 네트워크 구조는, Metric learning 을 함에 있어, 어떤 Mining function을 사용할 것이냐에 따른 것으로, anchor/positive/negative 를 뽑는 triplet mining 을 사용할 경우, triplet network 를 사용하게 되고, anchor/{positive, negative} 를 사용하는 경우, siamese network 를 사용하게 된다. Metric learning 특징 상, input data pair 가 들어가게 되고, 이 때 모델은 weight sharing 을 통해 parameter 의 갯수를 줄이고, 성능 향상에 기여한다고 한다.

3. metric loss function
metric learning 지원 패키지의 공식 문서를 보면 알 수 있 듯, 정말 많은 loss function 들이 있다. 하나씩 논문을 들춰보고 있는데, 조만간 loss function들을 특성 별로 묶어서 정리해보려 한다. 여기서는 survey 에서 언급한 몇 가지의 loss function 에 대해 이야기해보겠다.
3-1. contrastive loss function
해당 loss function 은 두 가지 input pair 를 사용하게 되며, 두 데이터의 라벨이 같을 경우 gamma 는 0 아닐 경우, 1 이 된다. (논문에서는 반대로 쓰여져 있는데, 오류가 있는 것 같다.) 흥미로운 점은, negative sample 에 대해서 margin 값보다 더 멀어지지 않게 하기 위해서, max 제약식을 둔 점이다. margin 정도로만 멀면 충분함으로, high variance gradient 를 방지하기 위함으로 보인다.

3-2. triplet loss function
계속해서 이야기해오던 triplet mining 에 따른 loss function 이다. anchor/positive/negative pair 가 필요하며, 흥미로운 점은 마지막에 있는 alpha 부분이다. 이 부분이 없어지만, anchor-positive, anchor-negative pair 간의 거리가 모두 같게 되는 문제가 발생하게 되는데, 이를 방지하기 위해서 존재한다고 한다.

3-3. angular loss function
논문을 굉장히 흥미롭게 읽었는데, triplet loss function 의 경우, anchor 와 positive, anchor 와 negative 간의 짝을 보지만, 3가지 위치를 동시에 보지 못하는 문제가 발생함에 따라, 한 쪽을 optimize 하면서 다른 한 쪽의 적합한 거리가 보장받지 못하는 경우가 발생하였는데, 세 가지 데이터 포인트 간 거리를, 삼각형의 각(angle) 의 관점에서 보면서, negative data point 가 가지고 있는 내각에 조건을 주는 방식을 사용한다. 해당 loss function을 통해서, anchor/positive/negative 세 데이터 포인트가 요구하는 거리 조건을 동시에 충족시키면서 모델을 최적화할 수 있게 된다.
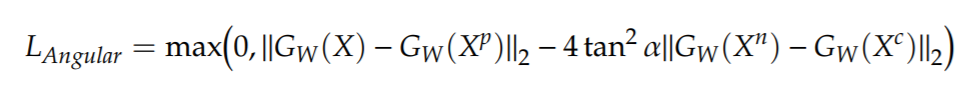
Conclusion
Metric Learning 이 사용된 이전 연구들의 토픽을 살펴 보니, retrieval task 와 recognition/identification task 가 상당수로 많았다. 사실 상, informative sample selection 에서 비효율이 많이 발생하다보니, Metric Learning 에 적합한 task 라는 것이 분명하지 않은 이상, 시도하기 쉽지 않은 것 같기도 하다. 하지만, imbalanced data 에 강하고, 유사도를 직접 학습하는 방식은 transfer learning 에 필요한 pretraining에 효과적이기 때문에, 해당 metric learning task 에서 끝나지 않고, 이어 지는 fine-tuning task 가 있을 때, 더욱 유용해보인다.
Further research
1. embedding after classification vs embedding after metric learning
2. check the data cluster aspect of small label data
3. curriculum learning in metric learning
4. schematize the loss functions depends on their characters
'[논문 정리]' 카테고리의 다른 글
| [논문 정리] Translation in Multi-modal Learning 논문 정리 (0) | 2021.06.23 |
|---|---|
| [논문 정리] mixup: BEYOND EMPIRICAL RISK MINIMIZATION (0) | 2021.06.11 |
| [논문 정리] Learning both Weights and Connections for Efficient Neural Networks (0) | 2021.06.01 |
| [논문 정리] Intriguing properties of neural networks (0) | 2021.02.22 |
| [논문 정리] Generative Adversarial Networks (0) | 2021.01.17 |




